Ggtkuk

インボリュート曲線（インボリュートきょくせん）は、その法線が常に一つの定円に接するような平面曲線である。円の伸開線 (involute of circle) あるいは反クロソイド (anti-clothoid) とも呼ばれる。固定されて回転しない円形のリールに巻き取られた糸を弛まないように引き、ほどいていくと、糸の端点はインボリュート曲線を描く。

概要

• 
  

  

  
  

  
  

  インボリュート曲線
  

  
  

  
  


• 
  

  

  
  

  
  

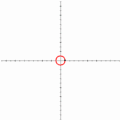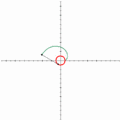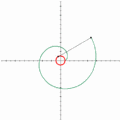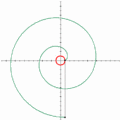
  糸を解く様子
  

  
  

  
  


• 
  

  

  
  

  
  

  伸開線の法線と円の接線
  

  
  

  
  

これを初めて研究したのはホイヘンスである。ホイヘンスは等時性を示す擺線振子を作るために、円の伸開線を用いた。

媒介変数表示では

{x=a(cos⁡θ+θsin⁡θ),y=a(sin⁡θ−θcos⁡θ){displaystyle {begin{cases}x=a(cos theta +theta sin theta ),\y=a(sin theta -theta cos theta )end{cases}}}

で表される。代数螺旋 (アルキメデスの螺旋) と曲線の形状は似ているが、同一ではない。

応用

一つの円とそれに接する一つの直線を取る。円に沿って直線を滑ることなく回転させるとき、直線上の任意の点が描く軌跡は円の伸開線と相似になる。

運動学的に見れば、速度と回転速度を一定に保ったまま運動する物体の描く軌跡が円の伸開線となる。速度が一定で、回転速度が線型に増加する物体が描く軌跡がクロソイドであることから、円の伸開線の別名として反クロソイドの名がある。

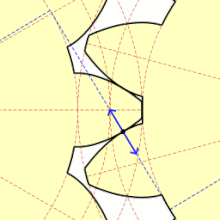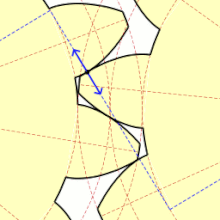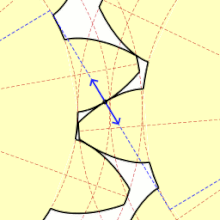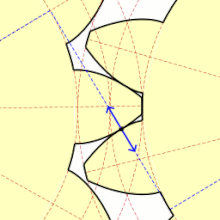
インボリュート歯車の歯の接触面

歯車の歯の形には円の伸開線の一部が使われている（インボリュート歯車）。これは、二つの歯が接する点における接線が共通するような形になっているため、歯車の回転速度が一定になり、歯車の間のエネルギー伝導が最適になることが望めるからである。このような歯車に関して、他にも様々な注目すべき性質がある。

エアコンの室外機であるコンプレッサー（圧縮機）には、スクロール方式が採用されている。固定スクロールと可動スクロールはインボリュート曲線が使われている^[1]。

脚注

関連項目

• 歯車


• クロソイド


• 螺旋


• 伸開線

外部リンク

• Weisstein, Eric W. "Circle Involute". MathWorld（英語）..mw-parser-output cite.citation{font-style:inherit}.mw-parser-output .citation q{quotes:"""""""'""'"}.mw-parser-output .citation .cs1-lock-free a{background:url("//upload.wikimedia.org/wikipedia/commons/thumb/6/65/Lock-green.svg/9px-Lock-green.svg.png")no-repeat;background-position:right .1em center}.mw-parser-output .citation .cs1-lock-limited a,.mw-parser-output .citation .cs1-lock-registration a{background:url("//upload.wikimedia.org/wikipedia/commons/thumb/d/d6/Lock-gray-alt-2.svg/9px-Lock-gray-alt-2.svg.png")no-repeat;background-position:right .1em center}.mw-parser-output .citation .cs1-lock-subscription a{background:url("//upload.wikimedia.org/wikipedia/commons/thumb/a/aa/Lock-red-alt-2.svg/9px-Lock-red-alt-2.svg.png")no-repeat;background-position:right .1em center}.mw-parser-output .cs1-subscription,.mw-parser-output .cs1-registration{color:#555}.mw-parser-output .cs1-subscription span,.mw-parser-output .cs1-registration span{border-bottom:1px dotted;cursor:help}.mw-parser-output .cs1-ws-icon a{background:url("//upload.wikimedia.org/wikipedia/commons/thumb/4/4c/Wikisource-logo.svg/12px-Wikisource-logo.svg.png")no-repeat;background-position:right .1em center}.mw-parser-output code.cs1-code{color:inherit;background:inherit;border:inherit;padding:inherit}.mw-parser-output .cs1-hidden-error{display:none;font-size:100%}.mw-parser-output .cs1-visible-error{font-size:100%}.mw-parser-output .cs1-maint{display:none;color:#33aa33;margin-left:0.3em}.mw-parser-output .cs1-subscription,.mw-parser-output .cs1-registration,.mw-parser-output .cs1-format{font-size:95%}.mw-parser-output .cs1-kern-left,.mw-parser-output .cs1-kern-wl-left{padding-left:0.2em}.mw-parser-output .cs1-kern-right,.mw-parser-output .cs1-kern-wl-right{padding-right:0.2em}


• Mathcurve.com, 円の伸開線（仏語）