Closed-form expression for certain product
$begingroup$
$mathrm G$ is Catalan's constant.
I recently found the product
$$
alpha=prod_{n=1}^{infty}frac{E_n(frac12)E_n(frac7{12})E_n(frac1{20})E_n(frac{13}{20})}{E_n(frac14)E_n(frac1{12})E_n(frac3{20})E_n(frac{11}{20})}=\
expleft[frac{47mathrm G}{30pi}+frac34right]sqrt{frac{33}{91pi}sqrt{frac2pifrac{sqrt[5]{11}}{sqrt[3]{7}}sqrt[5]{frac{3^3}{13^{3}}}}}$$
Where $$E_n(x)=frac{j(n+x)}{(en)^{2x}j(n-x)}qquad xin(0,1)$$
and $j(x)=x^x$.
Could I have some numerical evidence, or better yet an alternate proof? My tools are limited to desmos, which cannot really handle infinite products. Thanks.
My Proof.
We define $$mathrm L(x)=frac1piint_0^{pi x}log(sin t)dt$$
And we use $$sin t=tprod_{ngeq1}left(1-frac{t^2}{pi^2 n^2}right)$$
To see that $$log(sin t)=log(t)+sum_{ngeq1}logfrac{pi^2n^2-t^2}{pi^2n^2}$$
Then integrate both sides over $[0,x]$ to get
$$pimathrm L(x/pi)=x(log x-1)+sum_{ngeq1}xlogbigg(1-frac{x^2}{pi^2n^2}bigg)-2x+pi nlogfrac{pi n+x}{pi n-x}$$
$$pimathrm L(x/pi)=logleft[frac{j(x)}{e^x}right]+sum_{ngeq1}logleft[frac{j(pi n+x)}{(epi n)^{2x}j(pi n-x)}right]$$
$xmapsto pi x$:
$$pimathrm L(x)=logleft[frac{j(pi x)}{e^{pi x}}right]+sum_{ngeq1}logleft[frac{j(pi n+pi x)}{(epi n)^{2pi x}j(pi n-pi x)}right]$$
$$mathrm L(x)=logleft[left(fracpi{e}right)^xj(x)right]+sum_{ngeq1}log E_n(x)$$
Then we define $$U(x)=prod_{ngeq1}E_n(x)$$
To see that $$U(x)=left(frac{e}{pi x}right)^xexpmathrm L(x)$$
Where we used $$sum_{n}log(a_n)=logleft[prod_{n}a_nright]$$
and the neat rules $$log(a^b)=log(e^{blog a})=blog a$$
$$log(a)pm b=logleft(e^{pm b}aright)$$
to simplify the expressions. Next, we define
$$P_{mu,nu}(a_1,a_2,dots,a_mu;b_1,b_2,dots,b_nu)=frac{prod_{i=1}^mu U(a_i)}{prod_{i=1}^nu U(b_i)}$$
And we see that
$$P_{mu,nu}(a_1,dots,a_mu;b_1,dots,b_nu)=prod_{ngeq1}frac{prod_{i=1}^mu E_n(a_i)}{prod_{i=1}^nu E_n(b_i)}$$
This gives $$P_{1,1}(x_1;x_2)=left(frac{e}{pi}right)^{x_1-x_2}frac{j(x_2)}{j(x_1)}expleft[mathrm L(x_1)-mathrm L(x_2)right]$$
Then we define $$mathrm{T}(x)=frac{1}{pi}int_0^{pi x}log(tan t)dt=mathrm L(x)-mathrm L(x+1/2)-frac12log2$$
To get that
$$P_{1,1}left(x;x+frac12right)=sqrt{frac{2pi}e},frac{j(x+1/2)}{j(x)}expmathrm T(x)$$
So we have
$$P_{2,2}left(x_1,x_2+frac12 ;x_2,x_1+frac12right)=frac{j(x_1+1/2)j(x_2)}{j(x_2+1/2)j(x_1)}expleft[mathrm T(x_1)-mathrm T(x_2)right]$$
Then using the identities
$$mathrm L(1/2)=-frac12log2$$
$$mathrm L(1/4)=frac{mathrm G}{2pi}-frac14log2$$
We get $$P_{1,1}left(frac12;frac14right)=frac1{(2pi)^{1/4}}expleft[frac{mathrm G}{2pi}+frac14right]tag{1}$$
From here, the identity
$$-mathrm T(1/12)=frac{2mathrm G}{3pi}$$
which gives
$$P_{1,1}left(frac7{12};frac1{12}right)=sqrt{frac6{7pisqrt[6]{7}}}expleft[frac{2mathrm G}{3pi}+frac12right]tag{2}$$
Then from here, the identity
$$mathrm T(1/20)-mathrm T(3/20)=frac{2mathrm G}{5pi}$$
gives $$P_{2,2}left(frac1{20},frac{13}{20};frac3{20},frac{11}{20}right)=left(frac{j(11)j(3)}{j(13)}right)^{1/20}expfrac{2mathrm G}{5pi}tag{3}$$
Then multiplying $(1),(2),$ and $(3)$, we have the desired result, namely
$$P_{4,4}left(frac12,frac7{12},frac1{20},frac{13}{20};frac14,frac1{12},frac3{20},frac{11}{20}right)=alpha$$
integration alternative-proof products
New contributor
clathratus is a new contributor to this site. Take care in asking for clarification, commenting, and answering.
Check out our Code of Conduct.
$endgroup$
add a comment |
$begingroup$
$mathrm G$ is Catalan's constant.
I recently found the product
$$
alpha=prod_{n=1}^{infty}frac{E_n(frac12)E_n(frac7{12})E_n(frac1{20})E_n(frac{13}{20})}{E_n(frac14)E_n(frac1{12})E_n(frac3{20})E_n(frac{11}{20})}=\
expleft[frac{47mathrm G}{30pi}+frac34right]sqrt{frac{33}{91pi}sqrt{frac2pifrac{sqrt[5]{11}}{sqrt[3]{7}}sqrt[5]{frac{3^3}{13^{3}}}}}$$
Where $$E_n(x)=frac{j(n+x)}{(en)^{2x}j(n-x)}qquad xin(0,1)$$
and $j(x)=x^x$.
Could I have some numerical evidence, or better yet an alternate proof? My tools are limited to desmos, which cannot really handle infinite products. Thanks.
My Proof.
We define $$mathrm L(x)=frac1piint_0^{pi x}log(sin t)dt$$
And we use $$sin t=tprod_{ngeq1}left(1-frac{t^2}{pi^2 n^2}right)$$
To see that $$log(sin t)=log(t)+sum_{ngeq1}logfrac{pi^2n^2-t^2}{pi^2n^2}$$
Then integrate both sides over $[0,x]$ to get
$$pimathrm L(x/pi)=x(log x-1)+sum_{ngeq1}xlogbigg(1-frac{x^2}{pi^2n^2}bigg)-2x+pi nlogfrac{pi n+x}{pi n-x}$$
$$pimathrm L(x/pi)=logleft[frac{j(x)}{e^x}right]+sum_{ngeq1}logleft[frac{j(pi n+x)}{(epi n)^{2x}j(pi n-x)}right]$$
$xmapsto pi x$:
$$pimathrm L(x)=logleft[frac{j(pi x)}{e^{pi x}}right]+sum_{ngeq1}logleft[frac{j(pi n+pi x)}{(epi n)^{2pi x}j(pi n-pi x)}right]$$
$$mathrm L(x)=logleft[left(fracpi{e}right)^xj(x)right]+sum_{ngeq1}log E_n(x)$$
Then we define $$U(x)=prod_{ngeq1}E_n(x)$$
To see that $$U(x)=left(frac{e}{pi x}right)^xexpmathrm L(x)$$
Where we used $$sum_{n}log(a_n)=logleft[prod_{n}a_nright]$$
and the neat rules $$log(a^b)=log(e^{blog a})=blog a$$
$$log(a)pm b=logleft(e^{pm b}aright)$$
to simplify the expressions. Next, we define
$$P_{mu,nu}(a_1,a_2,dots,a_mu;b_1,b_2,dots,b_nu)=frac{prod_{i=1}^mu U(a_i)}{prod_{i=1}^nu U(b_i)}$$
And we see that
$$P_{mu,nu}(a_1,dots,a_mu;b_1,dots,b_nu)=prod_{ngeq1}frac{prod_{i=1}^mu E_n(a_i)}{prod_{i=1}^nu E_n(b_i)}$$
This gives $$P_{1,1}(x_1;x_2)=left(frac{e}{pi}right)^{x_1-x_2}frac{j(x_2)}{j(x_1)}expleft[mathrm L(x_1)-mathrm L(x_2)right]$$
Then we define $$mathrm{T}(x)=frac{1}{pi}int_0^{pi x}log(tan t)dt=mathrm L(x)-mathrm L(x+1/2)-frac12log2$$
To get that
$$P_{1,1}left(x;x+frac12right)=sqrt{frac{2pi}e},frac{j(x+1/2)}{j(x)}expmathrm T(x)$$
So we have
$$P_{2,2}left(x_1,x_2+frac12 ;x_2,x_1+frac12right)=frac{j(x_1+1/2)j(x_2)}{j(x_2+1/2)j(x_1)}expleft[mathrm T(x_1)-mathrm T(x_2)right]$$
Then using the identities
$$mathrm L(1/2)=-frac12log2$$
$$mathrm L(1/4)=frac{mathrm G}{2pi}-frac14log2$$
We get $$P_{1,1}left(frac12;frac14right)=frac1{(2pi)^{1/4}}expleft[frac{mathrm G}{2pi}+frac14right]tag{1}$$
From here, the identity
$$-mathrm T(1/12)=frac{2mathrm G}{3pi}$$
which gives
$$P_{1,1}left(frac7{12};frac1{12}right)=sqrt{frac6{7pisqrt[6]{7}}}expleft[frac{2mathrm G}{3pi}+frac12right]tag{2}$$
Then from here, the identity
$$mathrm T(1/20)-mathrm T(3/20)=frac{2mathrm G}{5pi}$$
gives $$P_{2,2}left(frac1{20},frac{13}{20};frac3{20},frac{11}{20}right)=left(frac{j(11)j(3)}{j(13)}right)^{1/20}expfrac{2mathrm G}{5pi}tag{3}$$
Then multiplying $(1),(2),$ and $(3)$, we have the desired result, namely
$$P_{4,4}left(frac12,frac7{12},frac1{20},frac{13}{20};frac14,frac1{12},frac3{20},frac{11}{20}right)=alpha$$
integration alternative-proof products
New contributor
clathratus is a new contributor to this site. Take care in asking for clarification, commenting, and answering.
Check out our Code of Conduct.
$endgroup$
add a comment |
$begingroup$
$mathrm G$ is Catalan's constant.
I recently found the product
$$
alpha=prod_{n=1}^{infty}frac{E_n(frac12)E_n(frac7{12})E_n(frac1{20})E_n(frac{13}{20})}{E_n(frac14)E_n(frac1{12})E_n(frac3{20})E_n(frac{11}{20})}=\
expleft[frac{47mathrm G}{30pi}+frac34right]sqrt{frac{33}{91pi}sqrt{frac2pifrac{sqrt[5]{11}}{sqrt[3]{7}}sqrt[5]{frac{3^3}{13^{3}}}}}$$
Where $$E_n(x)=frac{j(n+x)}{(en)^{2x}j(n-x)}qquad xin(0,1)$$
and $j(x)=x^x$.
Could I have some numerical evidence, or better yet an alternate proof? My tools are limited to desmos, which cannot really handle infinite products. Thanks.
My Proof.
We define $$mathrm L(x)=frac1piint_0^{pi x}log(sin t)dt$$
And we use $$sin t=tprod_{ngeq1}left(1-frac{t^2}{pi^2 n^2}right)$$
To see that $$log(sin t)=log(t)+sum_{ngeq1}logfrac{pi^2n^2-t^2}{pi^2n^2}$$
Then integrate both sides over $[0,x]$ to get
$$pimathrm L(x/pi)=x(log x-1)+sum_{ngeq1}xlogbigg(1-frac{x^2}{pi^2n^2}bigg)-2x+pi nlogfrac{pi n+x}{pi n-x}$$
$$pimathrm L(x/pi)=logleft[frac{j(x)}{e^x}right]+sum_{ngeq1}logleft[frac{j(pi n+x)}{(epi n)^{2x}j(pi n-x)}right]$$
$xmapsto pi x$:
$$pimathrm L(x)=logleft[frac{j(pi x)}{e^{pi x}}right]+sum_{ngeq1}logleft[frac{j(pi n+pi x)}{(epi n)^{2pi x}j(pi n-pi x)}right]$$
$$mathrm L(x)=logleft[left(fracpi{e}right)^xj(x)right]+sum_{ngeq1}log E_n(x)$$
Then we define $$U(x)=prod_{ngeq1}E_n(x)$$
To see that $$U(x)=left(frac{e}{pi x}right)^xexpmathrm L(x)$$
Where we used $$sum_{n}log(a_n)=logleft[prod_{n}a_nright]$$
and the neat rules $$log(a^b)=log(e^{blog a})=blog a$$
$$log(a)pm b=logleft(e^{pm b}aright)$$
to simplify the expressions. Next, we define
$$P_{mu,nu}(a_1,a_2,dots,a_mu;b_1,b_2,dots,b_nu)=frac{prod_{i=1}^mu U(a_i)}{prod_{i=1}^nu U(b_i)}$$
And we see that
$$P_{mu,nu}(a_1,dots,a_mu;b_1,dots,b_nu)=prod_{ngeq1}frac{prod_{i=1}^mu E_n(a_i)}{prod_{i=1}^nu E_n(b_i)}$$
This gives $$P_{1,1}(x_1;x_2)=left(frac{e}{pi}right)^{x_1-x_2}frac{j(x_2)}{j(x_1)}expleft[mathrm L(x_1)-mathrm L(x_2)right]$$
Then we define $$mathrm{T}(x)=frac{1}{pi}int_0^{pi x}log(tan t)dt=mathrm L(x)-mathrm L(x+1/2)-frac12log2$$
To get that
$$P_{1,1}left(x;x+frac12right)=sqrt{frac{2pi}e},frac{j(x+1/2)}{j(x)}expmathrm T(x)$$
So we have
$$P_{2,2}left(x_1,x_2+frac12 ;x_2,x_1+frac12right)=frac{j(x_1+1/2)j(x_2)}{j(x_2+1/2)j(x_1)}expleft[mathrm T(x_1)-mathrm T(x_2)right]$$
Then using the identities
$$mathrm L(1/2)=-frac12log2$$
$$mathrm L(1/4)=frac{mathrm G}{2pi}-frac14log2$$
We get $$P_{1,1}left(frac12;frac14right)=frac1{(2pi)^{1/4}}expleft[frac{mathrm G}{2pi}+frac14right]tag{1}$$
From here, the identity
$$-mathrm T(1/12)=frac{2mathrm G}{3pi}$$
which gives
$$P_{1,1}left(frac7{12};frac1{12}right)=sqrt{frac6{7pisqrt[6]{7}}}expleft[frac{2mathrm G}{3pi}+frac12right]tag{2}$$
Then from here, the identity
$$mathrm T(1/20)-mathrm T(3/20)=frac{2mathrm G}{5pi}$$
gives $$P_{2,2}left(frac1{20},frac{13}{20};frac3{20},frac{11}{20}right)=left(frac{j(11)j(3)}{j(13)}right)^{1/20}expfrac{2mathrm G}{5pi}tag{3}$$
Then multiplying $(1),(2),$ and $(3)$, we have the desired result, namely
$$P_{4,4}left(frac12,frac7{12},frac1{20},frac{13}{20};frac14,frac1{12},frac3{20},frac{11}{20}right)=alpha$$
integration alternative-proof products
New contributor
clathratus is a new contributor to this site. Take care in asking for clarification, commenting, and answering.
Check out our Code of Conduct.
$endgroup$
$mathrm G$ is Catalan's constant.
I recently found the product
$$
alpha=prod_{n=1}^{infty}frac{E_n(frac12)E_n(frac7{12})E_n(frac1{20})E_n(frac{13}{20})}{E_n(frac14)E_n(frac1{12})E_n(frac3{20})E_n(frac{11}{20})}=\
expleft[frac{47mathrm G}{30pi}+frac34right]sqrt{frac{33}{91pi}sqrt{frac2pifrac{sqrt[5]{11}}{sqrt[3]{7}}sqrt[5]{frac{3^3}{13^{3}}}}}$$
Where $$E_n(x)=frac{j(n+x)}{(en)^{2x}j(n-x)}qquad xin(0,1)$$
and $j(x)=x^x$.
Could I have some numerical evidence, or better yet an alternate proof? My tools are limited to desmos, which cannot really handle infinite products. Thanks.
My Proof.
We define $$mathrm L(x)=frac1piint_0^{pi x}log(sin t)dt$$
And we use $$sin t=tprod_{ngeq1}left(1-frac{t^2}{pi^2 n^2}right)$$
To see that $$log(sin t)=log(t)+sum_{ngeq1}logfrac{pi^2n^2-t^2}{pi^2n^2}$$
Then integrate both sides over $[0,x]$ to get
$$pimathrm L(x/pi)=x(log x-1)+sum_{ngeq1}xlogbigg(1-frac{x^2}{pi^2n^2}bigg)-2x+pi nlogfrac{pi n+x}{pi n-x}$$
$$pimathrm L(x/pi)=logleft[frac{j(x)}{e^x}right]+sum_{ngeq1}logleft[frac{j(pi n+x)}{(epi n)^{2x}j(pi n-x)}right]$$
$xmapsto pi x$:
$$pimathrm L(x)=logleft[frac{j(pi x)}{e^{pi x}}right]+sum_{ngeq1}logleft[frac{j(pi n+pi x)}{(epi n)^{2pi x}j(pi n-pi x)}right]$$
$$mathrm L(x)=logleft[left(fracpi{e}right)^xj(x)right]+sum_{ngeq1}log E_n(x)$$
Then we define $$U(x)=prod_{ngeq1}E_n(x)$$
To see that $$U(x)=left(frac{e}{pi x}right)^xexpmathrm L(x)$$
Where we used $$sum_{n}log(a_n)=logleft[prod_{n}a_nright]$$
and the neat rules $$log(a^b)=log(e^{blog a})=blog a$$
$$log(a)pm b=logleft(e^{pm b}aright)$$
to simplify the expressions. Next, we define
$$P_{mu,nu}(a_1,a_2,dots,a_mu;b_1,b_2,dots,b_nu)=frac{prod_{i=1}^mu U(a_i)}{prod_{i=1}^nu U(b_i)}$$
And we see that
$$P_{mu,nu}(a_1,dots,a_mu;b_1,dots,b_nu)=prod_{ngeq1}frac{prod_{i=1}^mu E_n(a_i)}{prod_{i=1}^nu E_n(b_i)}$$
This gives $$P_{1,1}(x_1;x_2)=left(frac{e}{pi}right)^{x_1-x_2}frac{j(x_2)}{j(x_1)}expleft[mathrm L(x_1)-mathrm L(x_2)right]$$
Then we define $$mathrm{T}(x)=frac{1}{pi}int_0^{pi x}log(tan t)dt=mathrm L(x)-mathrm L(x+1/2)-frac12log2$$
To get that
$$P_{1,1}left(x;x+frac12right)=sqrt{frac{2pi}e},frac{j(x+1/2)}{j(x)}expmathrm T(x)$$
So we have
$$P_{2,2}left(x_1,x_2+frac12 ;x_2,x_1+frac12right)=frac{j(x_1+1/2)j(x_2)}{j(x_2+1/2)j(x_1)}expleft[mathrm T(x_1)-mathrm T(x_2)right]$$
Then using the identities
$$mathrm L(1/2)=-frac12log2$$
$$mathrm L(1/4)=frac{mathrm G}{2pi}-frac14log2$$
We get $$P_{1,1}left(frac12;frac14right)=frac1{(2pi)^{1/4}}expleft[frac{mathrm G}{2pi}+frac14right]tag{1}$$
From here, the identity
$$-mathrm T(1/12)=frac{2mathrm G}{3pi}$$
which gives
$$P_{1,1}left(frac7{12};frac1{12}right)=sqrt{frac6{7pisqrt[6]{7}}}expleft[frac{2mathrm G}{3pi}+frac12right]tag{2}$$
Then from here, the identity
$$mathrm T(1/20)-mathrm T(3/20)=frac{2mathrm G}{5pi}$$
gives $$P_{2,2}left(frac1{20},frac{13}{20};frac3{20},frac{11}{20}right)=left(frac{j(11)j(3)}{j(13)}right)^{1/20}expfrac{2mathrm G}{5pi}tag{3}$$
Then multiplying $(1),(2),$ and $(3)$, we have the desired result, namely
$$P_{4,4}left(frac12,frac7{12},frac1{20},frac{13}{20};frac14,frac1{12},frac3{20},frac{11}{20}right)=alpha$$
integration alternative-proof products
integration alternative-proof products
New contributor
clathratus is a new contributor to this site. Take care in asking for clarification, commenting, and answering.
Check out our Code of Conduct.
New contributor
clathratus is a new contributor to this site. Take care in asking for clarification, commenting, and answering.
Check out our Code of Conduct.
edited 2 days ago
clathratus
New contributor
clathratus is a new contributor to this site. Take care in asking for clarification, commenting, and answering.
Check out our Code of Conduct.
asked 2 days ago
clathratusclathratus
1485
1485
New contributor
clathratus is a new contributor to this site. Take care in asking for clarification, commenting, and answering.
Check out our Code of Conduct.
New contributor
clathratus is a new contributor to this site. Take care in asking for clarification, commenting, and answering.
Check out our Code of Conduct.
clathratus is a new contributor to this site. Take care in asking for clarification, commenting, and answering.
Check out our Code of Conduct.
add a comment |
add a comment |
4 Answers
4
active
oldest
votes
$begingroup$
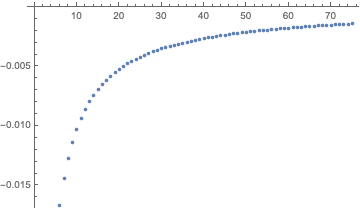
the OP asks for some numerical evidence: plotted below is the constant $alpha$ minus the $prod_{n=1}^N$ of the expression in OP, as a function of $N$; so at least within 1 part in 1000 the infinite product does seem to converge from above to the stated constant.
$endgroup$
1
$begingroup$
This is perfect, thank you. What software did you use to plot this?
$endgroup$
– clathratus
2 days ago
$begingroup$
The downvote is mine.
$endgroup$
– user64494
2 days ago
$begingroup$
oh, this is just Mathematica output.
$endgroup$
– Carlo Beenakker
2 days ago
add a comment |
$begingroup$
The following Mathematica code
NProduct[(1/2 + n)^(1/2 + n)/(Exp[1]*n)^(2*1/2)/(n - 1/2)^(n -
1/2)*(7/12 + n)^(7/12 + n)/(Exp[1]*n)^(2*7/12)/(n - 7/12)^(n -
7/12)*(1/20 + n)^(1/20 + n)/(Exp[1]*n)^(2*1/20)/(n - 1/20)^(n -
1/20)*(13/20 + n)^(13/20 + n)/(Exp[1]*n)^(2*13/20)/(n -13/20)^(n -13/20)/
((1/4 + n)^(1/4 + n)/(Exp[1]*n)^(2*1/4)/(n -
1/4)^(n - 1/4))/((1/12 + n)^(1/12 + n)/(Exp[1]*
n)^(2*1/12)/(n - 1/12)^(n - 1/12))/((11/20 + n)^(11/20 +
n)/(Exp[1]*n)^(2*11/20)/(n - 11/20)^(n - 11/20))/((3/20 +
n)^(3/20 + n)/(Exp[1]*n)^(2*3/20)/(n - 3/20)^(n - 3/20)),
{n,1,Infinity}, AccuracyGoal -> 3, WorkingPrecision -> 15]
performs
$0.78046 $
If somebody verifies the above code, it would be kind of her/him.
Addition. The Maple command for the product up to $100$
Digits:=15:evalf(product((1/2+n)^(1/2+n)*(7/12+n)^(7/12+n)*(1/20+n)^(1/20+n)*(13/20+n)^(13/20+n)*(n-1/4)^(n-1/4)*(n-1/12)^(n-1/12)*(n-11/20)^(n-11/20)*(n-3/20)^(n-3/20)/(exp(1)*n*(n-1/2)^(n-1/2)*sqrt(exp(1)*n)*(n-7/12)^(n-7/12)*(n-1/20)^(n-1/20)*(n-13/20)^(n-13/20)*(1/4+n)^(1/4+n)*(1/12+n)^(1/12+n)*(11/20+n)^(11/20+n)*(3/20+n)^(3/20+n)), n = 1 .. 100));
produces $0.781527175985084 $.
Also
N[Exp[47*Catalan/30/Pi + 3/4]* Sqrt[33/91/Pi*Sqrt[2/Pi*11^(1/5)/7^(1/3)*3^(3/5)/13^(3/5)]], 15]
$0.780459197412937 $
Edit. A typo in the codes ($(n-1/2)^{n-1/2}$ instead of $(n-1/2)^{n-1}$) is corrected. That typo leads to incorrect results.
$endgroup$
add a comment |
$begingroup$
Using the Maple code from user64494's answer (but using mul(evalf(...)) instead of evalf(product(...)) for greater efficiency, and 20 digits), I computed the product for 1000,2000,3000,4000 terms. It took about four minutes.
The answers were: 0.78056641010997748236, 0.78056641010997748236, 0.78056641010997748236, 0.78056641010997748236.
Now assuming that the product to $N$ terms has an asymptotic expansion $$a_0+a_1/N+a_2/N^2+a_3/N^3+cdots,$$ which can surely be proved but I didn't, extrapolation of these 4 values gives
$$a_0approx 0.7804591974129376479,a_1approx 0.107, a_2approx -0.0463, a_3approx 0.0151.$$
The value of $a_0$ agrees with the proposed infinite product 0.7804591974129374862 to 15 digits.
ADDED: By evaluating $x^x$ as evalf(x)^x, the same computation runs in about 20 seconds even with twice the precision. Adding the product with 5000 terms, agreement to 20 digits is obtained.
ADDED[2]: I don't know how it does it, but Maple's built-in code for numerical evaluation of infinite products takes mere seconds to confirm this to 200 digits.
$endgroup$
$begingroup$
Also really great! Thanks for all the hard effort! 20 digits of precision is good enough for me.
$endgroup$
– clathratus
yesterday
add a comment |
$begingroup$
Following off of @user64494, the Mathematica code
Product[(1/2 + n)^(1/2 + n)/(Exp[1]*n)^(2*1/2)/(n - 1/2)^(n -
1/2)*(7/12 + n)^(7/12 + n)/(Exp[1]*n)^(2*7/12)/(n - 7/12)^(n -
7/12)*(1/20 + n)^(1/20 + n)/(Exp[1]*n)^(2*1/20)/(n - 1/20)^(n -
1/20)*(13/20 + n)^(13/20 + n)/(Exp[1]*n)^(2*13/20)/(n -
13/20)^(n -
13/20)/((1/4 + n)^(1/4 + n)/(Exp[1]*n)^(2*1/4)/(n -
1/4)^(n - 1/4))/((1/12 + n)^(1/12 + n)/(Exp[1]*
n)^(2*1/12)/(n - 1/12)^(n - 1/12))/((11/20 + n)^(11/20 +
n)/(Exp[1]*n)^(2*11/20)/(n - 11/20)^(n - 11/20))/((3/20 +
n)^(3/20 + n)/(Exp[1]*n)^(2*3/20)/(n - 3/20)^(n - 3/20)), {n,
1, Infinity}]
gives the closed form output
$$frac{{2}^{1/4} 3^{13/20} 11^{11/20} 5^{frac{1}{5} zeta left(-1,-frac{1}{4}right)-frac{1}{480}} exp left(frac{1}{5} zeta ^{(1,0)}left(-1,-frac{1}{4}right)+zeta ^{(1,0)}left(-1,frac{19}{20}right)-zeta ^{(1,0)}left(-1,-frac{1}{20}right)+frac{97 C}{60 pi }+frac{361}{480}right)}{7^{7/12} 13^{13/20} pi ^{3/4} {Glaisher}^{1/40}}$$
where Glaisher's constant is approximately 1.28243 and $zeta$ is the (generalized) Riemann zeta function. Evaluating the above mess to 20 decimal places gives
$$0.780~459~197~412~937~486~21.$$
New contributor
erfink is a new contributor to this site. Take care in asking for clarification, commenting, and answering.
Check out our Code of Conduct.
$endgroup$
$begingroup$
Woah! I had no idea that Glaisher's constant was in here! Thanks.
$endgroup$
– clathratus
yesterday
add a comment |
Your Answer
StackExchange.ifUsing("editor", function () {
return StackExchange.using("mathjaxEditing", function () {
StackExchange.MarkdownEditor.creationCallbacks.add(function (editor, postfix) {
StackExchange.mathjaxEditing.prepareWmdForMathJax(editor, postfix, [["$", "$"], ["\\(","\\)"]]);
});
});
}, "mathjax-editing");
StackExchange.ready(function() {
var channelOptions = {
tags: "".split(" "),
id: "504"
};
initTagRenderer("".split(" "), "".split(" "), channelOptions);
StackExchange.using("externalEditor", function() {
// Have to fire editor after snippets, if snippets enabled
if (StackExchange.settings.snippets.snippetsEnabled) {
StackExchange.using("snippets", function() {
createEditor();
});
}
else {
createEditor();
}
});
function createEditor() {
StackExchange.prepareEditor({
heartbeatType: 'answer',
autoActivateHeartbeat: false,
convertImagesToLinks: true,
noModals: true,
showLowRepImageUploadWarning: true,
reputationToPostImages: 10,
bindNavPrevention: true,
postfix: "",
imageUploader: {
brandingHtml: "Powered by u003ca class="icon-imgur-white" href="https://imgur.com/"u003eu003c/au003e",
contentPolicyHtml: "User contributions licensed under u003ca href="https://creativecommons.org/licenses/by-sa/3.0/"u003ecc by-sa 3.0 with attribution requiredu003c/au003e u003ca href="https://stackoverflow.com/legal/content-policy"u003e(content policy)u003c/au003e",
allowUrls: true
},
noCode: true, onDemand: true,
discardSelector: ".discard-answer"
,immediatelyShowMarkdownHelp:true
});
}
});
clathratus is a new contributor. Be nice, and check out our Code of Conduct.
Sign up or log in
StackExchange.ready(function () {
StackExchange.helpers.onClickDraftSave('#login-link');
});
Sign up using Google
Sign up using Facebook
Sign up using Email and Password
Post as a guest
Required, but never shown
StackExchange.ready(
function () {
StackExchange.openid.initPostLogin('.new-post-login', 'https%3a%2f%2fmathoverflow.net%2fquestions%2f326156%2fclosed-form-expression-for-certain-product%23new-answer', 'question_page');
}
);
Post as a guest
Required, but never shown
4 Answers
4
active
oldest
votes
4 Answers
4
active
oldest
votes
active
oldest
votes
active
oldest
votes
$begingroup$
the OP asks for some numerical evidence: plotted below is the constant $alpha$ minus the $prod_{n=1}^N$ of the expression in OP, as a function of $N$; so at least within 1 part in 1000 the infinite product does seem to converge from above to the stated constant.

$endgroup$
1
$begingroup$
This is perfect, thank you. What software did you use to plot this?
$endgroup$
– clathratus
2 days ago
$begingroup$
The downvote is mine.
$endgroup$
– user64494
2 days ago
$begingroup$
oh, this is just Mathematica output.
$endgroup$
– Carlo Beenakker
2 days ago
add a comment |
$begingroup$
the OP asks for some numerical evidence: plotted below is the constant $alpha$ minus the $prod_{n=1}^N$ of the expression in OP, as a function of $N$; so at least within 1 part in 1000 the infinite product does seem to converge from above to the stated constant.

$endgroup$
1
$begingroup$
This is perfect, thank you. What software did you use to plot this?
$endgroup$
– clathratus
2 days ago
$begingroup$
The downvote is mine.
$endgroup$
– user64494
2 days ago
$begingroup$
oh, this is just Mathematica output.
$endgroup$
– Carlo Beenakker
2 days ago
add a comment |
$begingroup$
the OP asks for some numerical evidence: plotted below is the constant $alpha$ minus the $prod_{n=1}^N$ of the expression in OP, as a function of $N$; so at least within 1 part in 1000 the infinite product does seem to converge from above to the stated constant.

$endgroup$
the OP asks for some numerical evidence: plotted below is the constant $alpha$ minus the $prod_{n=1}^N$ of the expression in OP, as a function of $N$; so at least within 1 part in 1000 the infinite product does seem to converge from above to the stated constant.

edited 2 days ago
answered 2 days ago
Carlo BeenakkerCarlo Beenakker
79k9187290
79k9187290
1
$begingroup$
This is perfect, thank you. What software did you use to plot this?
$endgroup$
– clathratus
2 days ago
$begingroup$
The downvote is mine.
$endgroup$
– user64494
2 days ago
$begingroup$
oh, this is just Mathematica output.
$endgroup$
– Carlo Beenakker
2 days ago
add a comment |
1
$begingroup$
This is perfect, thank you. What software did you use to plot this?
$endgroup$
– clathratus
2 days ago
$begingroup$
The downvote is mine.
$endgroup$
– user64494
2 days ago
$begingroup$
oh, this is just Mathematica output.
$endgroup$
– Carlo Beenakker
2 days ago
1
1
$begingroup$
This is perfect, thank you. What software did you use to plot this?
$endgroup$
– clathratus
2 days ago
$begingroup$
This is perfect, thank you. What software did you use to plot this?
$endgroup$
– clathratus
2 days ago
$begingroup$
The downvote is mine.
$endgroup$
– user64494
2 days ago
$begingroup$
The downvote is mine.
$endgroup$
– user64494
2 days ago
$begingroup$
oh, this is just Mathematica output.
$endgroup$
– Carlo Beenakker
2 days ago
$begingroup$
oh, this is just Mathematica output.
$endgroup$
– Carlo Beenakker
2 days ago
add a comment |
$begingroup$
The following Mathematica code
NProduct[(1/2 + n)^(1/2 + n)/(Exp[1]*n)^(2*1/2)/(n - 1/2)^(n -
1/2)*(7/12 + n)^(7/12 + n)/(Exp[1]*n)^(2*7/12)/(n - 7/12)^(n -
7/12)*(1/20 + n)^(1/20 + n)/(Exp[1]*n)^(2*1/20)/(n - 1/20)^(n -
1/20)*(13/20 + n)^(13/20 + n)/(Exp[1]*n)^(2*13/20)/(n -13/20)^(n -13/20)/
((1/4 + n)^(1/4 + n)/(Exp[1]*n)^(2*1/4)/(n -
1/4)^(n - 1/4))/((1/12 + n)^(1/12 + n)/(Exp[1]*
n)^(2*1/12)/(n - 1/12)^(n - 1/12))/((11/20 + n)^(11/20 +
n)/(Exp[1]*n)^(2*11/20)/(n - 11/20)^(n - 11/20))/((3/20 +
n)^(3/20 + n)/(Exp[1]*n)^(2*3/20)/(n - 3/20)^(n - 3/20)),
{n,1,Infinity}, AccuracyGoal -> 3, WorkingPrecision -> 15]
performs
$0.78046 $
If somebody verifies the above code, it would be kind of her/him.
Addition. The Maple command for the product up to $100$
Digits:=15:evalf(product((1/2+n)^(1/2+n)*(7/12+n)^(7/12+n)*(1/20+n)^(1/20+n)*(13/20+n)^(13/20+n)*(n-1/4)^(n-1/4)*(n-1/12)^(n-1/12)*(n-11/20)^(n-11/20)*(n-3/20)^(n-3/20)/(exp(1)*n*(n-1/2)^(n-1/2)*sqrt(exp(1)*n)*(n-7/12)^(n-7/12)*(n-1/20)^(n-1/20)*(n-13/20)^(n-13/20)*(1/4+n)^(1/4+n)*(1/12+n)^(1/12+n)*(11/20+n)^(11/20+n)*(3/20+n)^(3/20+n)), n = 1 .. 100));
produces $0.781527175985084 $.
Also
N[Exp[47*Catalan/30/Pi + 3/4]* Sqrt[33/91/Pi*Sqrt[2/Pi*11^(1/5)/7^(1/3)*3^(3/5)/13^(3/5)]], 15]
$0.780459197412937 $
Edit. A typo in the codes ($(n-1/2)^{n-1/2}$ instead of $(n-1/2)^{n-1}$) is corrected. That typo leads to incorrect results.
$endgroup$
add a comment |
$begingroup$
The following Mathematica code
NProduct[(1/2 + n)^(1/2 + n)/(Exp[1]*n)^(2*1/2)/(n - 1/2)^(n -
1/2)*(7/12 + n)^(7/12 + n)/(Exp[1]*n)^(2*7/12)/(n - 7/12)^(n -
7/12)*(1/20 + n)^(1/20 + n)/(Exp[1]*n)^(2*1/20)/(n - 1/20)^(n -
1/20)*(13/20 + n)^(13/20 + n)/(Exp[1]*n)^(2*13/20)/(n -13/20)^(n -13/20)/
((1/4 + n)^(1/4 + n)/(Exp[1]*n)^(2*1/4)/(n -
1/4)^(n - 1/4))/((1/12 + n)^(1/12 + n)/(Exp[1]*
n)^(2*1/12)/(n - 1/12)^(n - 1/12))/((11/20 + n)^(11/20 +
n)/(Exp[1]*n)^(2*11/20)/(n - 11/20)^(n - 11/20))/((3/20 +
n)^(3/20 + n)/(Exp[1]*n)^(2*3/20)/(n - 3/20)^(n - 3/20)),
{n,1,Infinity}, AccuracyGoal -> 3, WorkingPrecision -> 15]
performs
$0.78046 $
If somebody verifies the above code, it would be kind of her/him.
Addition. The Maple command for the product up to $100$
Digits:=15:evalf(product((1/2+n)^(1/2+n)*(7/12+n)^(7/12+n)*(1/20+n)^(1/20+n)*(13/20+n)^(13/20+n)*(n-1/4)^(n-1/4)*(n-1/12)^(n-1/12)*(n-11/20)^(n-11/20)*(n-3/20)^(n-3/20)/(exp(1)*n*(n-1/2)^(n-1/2)*sqrt(exp(1)*n)*(n-7/12)^(n-7/12)*(n-1/20)^(n-1/20)*(n-13/20)^(n-13/20)*(1/4+n)^(1/4+n)*(1/12+n)^(1/12+n)*(11/20+n)^(11/20+n)*(3/20+n)^(3/20+n)), n = 1 .. 100));
produces $0.781527175985084 $.
Also
N[Exp[47*Catalan/30/Pi + 3/4]* Sqrt[33/91/Pi*Sqrt[2/Pi*11^(1/5)/7^(1/3)*3^(3/5)/13^(3/5)]], 15]
$0.780459197412937 $
Edit. A typo in the codes ($(n-1/2)^{n-1/2}$ instead of $(n-1/2)^{n-1}$) is corrected. That typo leads to incorrect results.
$endgroup$
add a comment |
$begingroup$
The following Mathematica code
NProduct[(1/2 + n)^(1/2 + n)/(Exp[1]*n)^(2*1/2)/(n - 1/2)^(n -
1/2)*(7/12 + n)^(7/12 + n)/(Exp[1]*n)^(2*7/12)/(n - 7/12)^(n -
7/12)*(1/20 + n)^(1/20 + n)/(Exp[1]*n)^(2*1/20)/(n - 1/20)^(n -
1/20)*(13/20 + n)^(13/20 + n)/(Exp[1]*n)^(2*13/20)/(n -13/20)^(n -13/20)/
((1/4 + n)^(1/4 + n)/(Exp[1]*n)^(2*1/4)/(n -
1/4)^(n - 1/4))/((1/12 + n)^(1/12 + n)/(Exp[1]*
n)^(2*1/12)/(n - 1/12)^(n - 1/12))/((11/20 + n)^(11/20 +
n)/(Exp[1]*n)^(2*11/20)/(n - 11/20)^(n - 11/20))/((3/20 +
n)^(3/20 + n)/(Exp[1]*n)^(2*3/20)/(n - 3/20)^(n - 3/20)),
{n,1,Infinity}, AccuracyGoal -> 3, WorkingPrecision -> 15]
performs
$0.78046 $
If somebody verifies the above code, it would be kind of her/him.
Addition. The Maple command for the product up to $100$
Digits:=15:evalf(product((1/2+n)^(1/2+n)*(7/12+n)^(7/12+n)*(1/20+n)^(1/20+n)*(13/20+n)^(13/20+n)*(n-1/4)^(n-1/4)*(n-1/12)^(n-1/12)*(n-11/20)^(n-11/20)*(n-3/20)^(n-3/20)/(exp(1)*n*(n-1/2)^(n-1/2)*sqrt(exp(1)*n)*(n-7/12)^(n-7/12)*(n-1/20)^(n-1/20)*(n-13/20)^(n-13/20)*(1/4+n)^(1/4+n)*(1/12+n)^(1/12+n)*(11/20+n)^(11/20+n)*(3/20+n)^(3/20+n)), n = 1 .. 100));
produces $0.781527175985084 $.
Also
N[Exp[47*Catalan/30/Pi + 3/4]* Sqrt[33/91/Pi*Sqrt[2/Pi*11^(1/5)/7^(1/3)*3^(3/5)/13^(3/5)]], 15]
$0.780459197412937 $
Edit. A typo in the codes ($(n-1/2)^{n-1/2}$ instead of $(n-1/2)^{n-1}$) is corrected. That typo leads to incorrect results.
$endgroup$
The following Mathematica code
NProduct[(1/2 + n)^(1/2 + n)/(Exp[1]*n)^(2*1/2)/(n - 1/2)^(n -
1/2)*(7/12 + n)^(7/12 + n)/(Exp[1]*n)^(2*7/12)/(n - 7/12)^(n -
7/12)*(1/20 + n)^(1/20 + n)/(Exp[1]*n)^(2*1/20)/(n - 1/20)^(n -
1/20)*(13/20 + n)^(13/20 + n)/(Exp[1]*n)^(2*13/20)/(n -13/20)^(n -13/20)/
((1/4 + n)^(1/4 + n)/(Exp[1]*n)^(2*1/4)/(n -
1/4)^(n - 1/4))/((1/12 + n)^(1/12 + n)/(Exp[1]*
n)^(2*1/12)/(n - 1/12)^(n - 1/12))/((11/20 + n)^(11/20 +
n)/(Exp[1]*n)^(2*11/20)/(n - 11/20)^(n - 11/20))/((3/20 +
n)^(3/20 + n)/(Exp[1]*n)^(2*3/20)/(n - 3/20)^(n - 3/20)),
{n,1,Infinity}, AccuracyGoal -> 3, WorkingPrecision -> 15]
performs
$0.78046 $
If somebody verifies the above code, it would be kind of her/him.
Addition. The Maple command for the product up to $100$
Digits:=15:evalf(product((1/2+n)^(1/2+n)*(7/12+n)^(7/12+n)*(1/20+n)^(1/20+n)*(13/20+n)^(13/20+n)*(n-1/4)^(n-1/4)*(n-1/12)^(n-1/12)*(n-11/20)^(n-11/20)*(n-3/20)^(n-3/20)/(exp(1)*n*(n-1/2)^(n-1/2)*sqrt(exp(1)*n)*(n-7/12)^(n-7/12)*(n-1/20)^(n-1/20)*(n-13/20)^(n-13/20)*(1/4+n)^(1/4+n)*(1/12+n)^(1/12+n)*(11/20+n)^(11/20+n)*(3/20+n)^(3/20+n)), n = 1 .. 100));
produces $0.781527175985084 $.
Also
N[Exp[47*Catalan/30/Pi + 3/4]* Sqrt[33/91/Pi*Sqrt[2/Pi*11^(1/5)/7^(1/3)*3^(3/5)/13^(3/5)]], 15]
$0.780459197412937 $
Edit. A typo in the codes ($(n-1/2)^{n-1/2}$ instead of $(n-1/2)^{n-1}$) is corrected. That typo leads to incorrect results.
edited 2 days ago
answered 2 days ago
user64494user64494
1,749517
1,749517
add a comment |
add a comment |
$begingroup$
Using the Maple code from user64494's answer (but using mul(evalf(...)) instead of evalf(product(...)) for greater efficiency, and 20 digits), I computed the product for 1000,2000,3000,4000 terms. It took about four minutes.
The answers were: 0.78056641010997748236, 0.78056641010997748236, 0.78056641010997748236, 0.78056641010997748236.
Now assuming that the product to $N$ terms has an asymptotic expansion $$a_0+a_1/N+a_2/N^2+a_3/N^3+cdots,$$ which can surely be proved but I didn't, extrapolation of these 4 values gives
$$a_0approx 0.7804591974129376479,a_1approx 0.107, a_2approx -0.0463, a_3approx 0.0151.$$
The value of $a_0$ agrees with the proposed infinite product 0.7804591974129374862 to 15 digits.
ADDED: By evaluating $x^x$ as evalf(x)^x, the same computation runs in about 20 seconds even with twice the precision. Adding the product with 5000 terms, agreement to 20 digits is obtained.
ADDED[2]: I don't know how it does it, but Maple's built-in code for numerical evaluation of infinite products takes mere seconds to confirm this to 200 digits.
$endgroup$
$begingroup$
Also really great! Thanks for all the hard effort! 20 digits of precision is good enough for me.
$endgroup$
– clathratus
yesterday
add a comment |
$begingroup$
Using the Maple code from user64494's answer (but using mul(evalf(...)) instead of evalf(product(...)) for greater efficiency, and 20 digits), I computed the product for 1000,2000,3000,4000 terms. It took about four minutes.
The answers were: 0.78056641010997748236, 0.78056641010997748236, 0.78056641010997748236, 0.78056641010997748236.
Now assuming that the product to $N$ terms has an asymptotic expansion $$a_0+a_1/N+a_2/N^2+a_3/N^3+cdots,$$ which can surely be proved but I didn't, extrapolation of these 4 values gives
$$a_0approx 0.7804591974129376479,a_1approx 0.107, a_2approx -0.0463, a_3approx 0.0151.$$
The value of $a_0$ agrees with the proposed infinite product 0.7804591974129374862 to 15 digits.
ADDED: By evaluating $x^x$ as evalf(x)^x, the same computation runs in about 20 seconds even with twice the precision. Adding the product with 5000 terms, agreement to 20 digits is obtained.
ADDED[2]: I don't know how it does it, but Maple's built-in code for numerical evaluation of infinite products takes mere seconds to confirm this to 200 digits.
$endgroup$
$begingroup$
Also really great! Thanks for all the hard effort! 20 digits of precision is good enough for me.
$endgroup$
– clathratus
yesterday
add a comment |
$begingroup$
Using the Maple code from user64494's answer (but using mul(evalf(...)) instead of evalf(product(...)) for greater efficiency, and 20 digits), I computed the product for 1000,2000,3000,4000 terms. It took about four minutes.
The answers were: 0.78056641010997748236, 0.78056641010997748236, 0.78056641010997748236, 0.78056641010997748236.
Now assuming that the product to $N$ terms has an asymptotic expansion $$a_0+a_1/N+a_2/N^2+a_3/N^3+cdots,$$ which can surely be proved but I didn't, extrapolation of these 4 values gives
$$a_0approx 0.7804591974129376479,a_1approx 0.107, a_2approx -0.0463, a_3approx 0.0151.$$
The value of $a_0$ agrees with the proposed infinite product 0.7804591974129374862 to 15 digits.
ADDED: By evaluating $x^x$ as evalf(x)^x, the same computation runs in about 20 seconds even with twice the precision. Adding the product with 5000 terms, agreement to 20 digits is obtained.
ADDED[2]: I don't know how it does it, but Maple's built-in code for numerical evaluation of infinite products takes mere seconds to confirm this to 200 digits.
$endgroup$
Using the Maple code from user64494's answer (but using mul(evalf(...)) instead of evalf(product(...)) for greater efficiency, and 20 digits), I computed the product for 1000,2000,3000,4000 terms. It took about four minutes.
The answers were: 0.78056641010997748236, 0.78056641010997748236, 0.78056641010997748236, 0.78056641010997748236.
Now assuming that the product to $N$ terms has an asymptotic expansion $$a_0+a_1/N+a_2/N^2+a_3/N^3+cdots,$$ which can surely be proved but I didn't, extrapolation of these 4 values gives
$$a_0approx 0.7804591974129376479,a_1approx 0.107, a_2approx -0.0463, a_3approx 0.0151.$$
The value of $a_0$ agrees with the proposed infinite product 0.7804591974129374862 to 15 digits.
ADDED: By evaluating $x^x$ as evalf(x)^x, the same computation runs in about 20 seconds even with twice the precision. Adding the product with 5000 terms, agreement to 20 digits is obtained.
ADDED[2]: I don't know how it does it, but Maple's built-in code for numerical evaluation of infinite products takes mere seconds to confirm this to 200 digits.
edited yesterday
answered 2 days ago
Brendan McKayBrendan McKay
25.4k152107
25.4k152107
$begingroup$
Also really great! Thanks for all the hard effort! 20 digits of precision is good enough for me.
$endgroup$
– clathratus
yesterday
add a comment |
$begingroup$
Also really great! Thanks for all the hard effort! 20 digits of precision is good enough for me.
$endgroup$
– clathratus
yesterday
$begingroup$
Also really great! Thanks for all the hard effort! 20 digits of precision is good enough for me.
$endgroup$
– clathratus
yesterday
$begingroup$
Also really great! Thanks for all the hard effort! 20 digits of precision is good enough for me.
$endgroup$
– clathratus
yesterday
add a comment |
$begingroup$
Following off of @user64494, the Mathematica code
Product[(1/2 + n)^(1/2 + n)/(Exp[1]*n)^(2*1/2)/(n - 1/2)^(n -
1/2)*(7/12 + n)^(7/12 + n)/(Exp[1]*n)^(2*7/12)/(n - 7/12)^(n -
7/12)*(1/20 + n)^(1/20 + n)/(Exp[1]*n)^(2*1/20)/(n - 1/20)^(n -
1/20)*(13/20 + n)^(13/20 + n)/(Exp[1]*n)^(2*13/20)/(n -
13/20)^(n -
13/20)/((1/4 + n)^(1/4 + n)/(Exp[1]*n)^(2*1/4)/(n -
1/4)^(n - 1/4))/((1/12 + n)^(1/12 + n)/(Exp[1]*
n)^(2*1/12)/(n - 1/12)^(n - 1/12))/((11/20 + n)^(11/20 +
n)/(Exp[1]*n)^(2*11/20)/(n - 11/20)^(n - 11/20))/((3/20 +
n)^(3/20 + n)/(Exp[1]*n)^(2*3/20)/(n - 3/20)^(n - 3/20)), {n,
1, Infinity}]
gives the closed form output
$$frac{{2}^{1/4} 3^{13/20} 11^{11/20} 5^{frac{1}{5} zeta left(-1,-frac{1}{4}right)-frac{1}{480}} exp left(frac{1}{5} zeta ^{(1,0)}left(-1,-frac{1}{4}right)+zeta ^{(1,0)}left(-1,frac{19}{20}right)-zeta ^{(1,0)}left(-1,-frac{1}{20}right)+frac{97 C}{60 pi }+frac{361}{480}right)}{7^{7/12} 13^{13/20} pi ^{3/4} {Glaisher}^{1/40}}$$
where Glaisher's constant is approximately 1.28243 and $zeta$ is the (generalized) Riemann zeta function. Evaluating the above mess to 20 decimal places gives
$$0.780~459~197~412~937~486~21.$$
New contributor
erfink is a new contributor to this site. Take care in asking for clarification, commenting, and answering.
Check out our Code of Conduct.
$endgroup$
$begingroup$
Woah! I had no idea that Glaisher's constant was in here! Thanks.
$endgroup$
– clathratus
yesterday
add a comment |
$begingroup$
Following off of @user64494, the Mathematica code
Product[(1/2 + n)^(1/2 + n)/(Exp[1]*n)^(2*1/2)/(n - 1/2)^(n -
1/2)*(7/12 + n)^(7/12 + n)/(Exp[1]*n)^(2*7/12)/(n - 7/12)^(n -
7/12)*(1/20 + n)^(1/20 + n)/(Exp[1]*n)^(2*1/20)/(n - 1/20)^(n -
1/20)*(13/20 + n)^(13/20 + n)/(Exp[1]*n)^(2*13/20)/(n -
13/20)^(n -
13/20)/((1/4 + n)^(1/4 + n)/(Exp[1]*n)^(2*1/4)/(n -
1/4)^(n - 1/4))/((1/12 + n)^(1/12 + n)/(Exp[1]*
n)^(2*1/12)/(n - 1/12)^(n - 1/12))/((11/20 + n)^(11/20 +
n)/(Exp[1]*n)^(2*11/20)/(n - 11/20)^(n - 11/20))/((3/20 +
n)^(3/20 + n)/(Exp[1]*n)^(2*3/20)/(n - 3/20)^(n - 3/20)), {n,
1, Infinity}]
gives the closed form output
$$frac{{2}^{1/4} 3^{13/20} 11^{11/20} 5^{frac{1}{5} zeta left(-1,-frac{1}{4}right)-frac{1}{480}} exp left(frac{1}{5} zeta ^{(1,0)}left(-1,-frac{1}{4}right)+zeta ^{(1,0)}left(-1,frac{19}{20}right)-zeta ^{(1,0)}left(-1,-frac{1}{20}right)+frac{97 C}{60 pi }+frac{361}{480}right)}{7^{7/12} 13^{13/20} pi ^{3/4} {Glaisher}^{1/40}}$$
where Glaisher's constant is approximately 1.28243 and $zeta$ is the (generalized) Riemann zeta function. Evaluating the above mess to 20 decimal places gives
$$0.780~459~197~412~937~486~21.$$
New contributor
erfink is a new contributor to this site. Take care in asking for clarification, commenting, and answering.
Check out our Code of Conduct.
$endgroup$
$begingroup$
Woah! I had no idea that Glaisher's constant was in here! Thanks.
$endgroup$
– clathratus
yesterday
add a comment |
$begingroup$
Following off of @user64494, the Mathematica code
Product[(1/2 + n)^(1/2 + n)/(Exp[1]*n)^(2*1/2)/(n - 1/2)^(n -
1/2)*(7/12 + n)^(7/12 + n)/(Exp[1]*n)^(2*7/12)/(n - 7/12)^(n -
7/12)*(1/20 + n)^(1/20 + n)/(Exp[1]*n)^(2*1/20)/(n - 1/20)^(n -
1/20)*(13/20 + n)^(13/20 + n)/(Exp[1]*n)^(2*13/20)/(n -
13/20)^(n -
13/20)/((1/4 + n)^(1/4 + n)/(Exp[1]*n)^(2*1/4)/(n -
1/4)^(n - 1/4))/((1/12 + n)^(1/12 + n)/(Exp[1]*
n)^(2*1/12)/(n - 1/12)^(n - 1/12))/((11/20 + n)^(11/20 +
n)/(Exp[1]*n)^(2*11/20)/(n - 11/20)^(n - 11/20))/((3/20 +
n)^(3/20 + n)/(Exp[1]*n)^(2*3/20)/(n - 3/20)^(n - 3/20)), {n,
1, Infinity}]
gives the closed form output
$$frac{{2}^{1/4} 3^{13/20} 11^{11/20} 5^{frac{1}{5} zeta left(-1,-frac{1}{4}right)-frac{1}{480}} exp left(frac{1}{5} zeta ^{(1,0)}left(-1,-frac{1}{4}right)+zeta ^{(1,0)}left(-1,frac{19}{20}right)-zeta ^{(1,0)}left(-1,-frac{1}{20}right)+frac{97 C}{60 pi }+frac{361}{480}right)}{7^{7/12} 13^{13/20} pi ^{3/4} {Glaisher}^{1/40}}$$
where Glaisher's constant is approximately 1.28243 and $zeta$ is the (generalized) Riemann zeta function. Evaluating the above mess to 20 decimal places gives
$$0.780~459~197~412~937~486~21.$$
New contributor
erfink is a new contributor to this site. Take care in asking for clarification, commenting, and answering.
Check out our Code of Conduct.
$endgroup$
Following off of @user64494, the Mathematica code
Product[(1/2 + n)^(1/2 + n)/(Exp[1]*n)^(2*1/2)/(n - 1/2)^(n -
1/2)*(7/12 + n)^(7/12 + n)/(Exp[1]*n)^(2*7/12)/(n - 7/12)^(n -
7/12)*(1/20 + n)^(1/20 + n)/(Exp[1]*n)^(2*1/20)/(n - 1/20)^(n -
1/20)*(13/20 + n)^(13/20 + n)/(Exp[1]*n)^(2*13/20)/(n -
13/20)^(n -
13/20)/((1/4 + n)^(1/4 + n)/(Exp[1]*n)^(2*1/4)/(n -
1/4)^(n - 1/4))/((1/12 + n)^(1/12 + n)/(Exp[1]*
n)^(2*1/12)/(n - 1/12)^(n - 1/12))/((11/20 + n)^(11/20 +
n)/(Exp[1]*n)^(2*11/20)/(n - 11/20)^(n - 11/20))/((3/20 +
n)^(3/20 + n)/(Exp[1]*n)^(2*3/20)/(n - 3/20)^(n - 3/20)), {n,
1, Infinity}]
gives the closed form output
$$frac{{2}^{1/4} 3^{13/20} 11^{11/20} 5^{frac{1}{5} zeta left(-1,-frac{1}{4}right)-frac{1}{480}} exp left(frac{1}{5} zeta ^{(1,0)}left(-1,-frac{1}{4}right)+zeta ^{(1,0)}left(-1,frac{19}{20}right)-zeta ^{(1,0)}left(-1,-frac{1}{20}right)+frac{97 C}{60 pi }+frac{361}{480}right)}{7^{7/12} 13^{13/20} pi ^{3/4} {Glaisher}^{1/40}}$$
where Glaisher's constant is approximately 1.28243 and $zeta$ is the (generalized) Riemann zeta function. Evaluating the above mess to 20 decimal places gives
$$0.780~459~197~412~937~486~21.$$
New contributor
erfink is a new contributor to this site. Take care in asking for clarification, commenting, and answering.
Check out our Code of Conduct.
edited yesterday
New contributor
erfink is a new contributor to this site. Take care in asking for clarification, commenting, and answering.
Check out our Code of Conduct.
answered yesterday
erfinkerfink
1315
1315
New contributor
erfink is a new contributor to this site. Take care in asking for clarification, commenting, and answering.
Check out our Code of Conduct.
New contributor
erfink is a new contributor to this site. Take care in asking for clarification, commenting, and answering.
Check out our Code of Conduct.
erfink is a new contributor to this site. Take care in asking for clarification, commenting, and answering.
Check out our Code of Conduct.
$begingroup$
Woah! I had no idea that Glaisher's constant was in here! Thanks.
$endgroup$
– clathratus
yesterday
add a comment |
$begingroup$
Woah! I had no idea that Glaisher's constant was in here! Thanks.
$endgroup$
– clathratus
yesterday
$begingroup$
Woah! I had no idea that Glaisher's constant was in here! Thanks.
$endgroup$
– clathratus
yesterday
$begingroup$
Woah! I had no idea that Glaisher's constant was in here! Thanks.
$endgroup$
– clathratus
yesterday
add a comment |
clathratus is a new contributor. Be nice, and check out our Code of Conduct.
clathratus is a new contributor. Be nice, and check out our Code of Conduct.
clathratus is a new contributor. Be nice, and check out our Code of Conduct.
clathratus is a new contributor. Be nice, and check out our Code of Conduct.
Thanks for contributing an answer to MathOverflow!
- Please be sure to answer the question. Provide details and share your research!
But avoid …
- Asking for help, clarification, or responding to other answers.
- Making statements based on opinion; back them up with references or personal experience.
Use MathJax to format equations. MathJax reference.
To learn more, see our tips on writing great answers.
Sign up or log in
StackExchange.ready(function () {
StackExchange.helpers.onClickDraftSave('#login-link');
});
Sign up using Google
Sign up using Facebook
Sign up using Email and Password
Post as a guest
Required, but never shown
StackExchange.ready(
function () {
StackExchange.openid.initPostLogin('.new-post-login', 'https%3a%2f%2fmathoverflow.net%2fquestions%2f326156%2fclosed-form-expression-for-certain-product%23new-answer', 'question_page');
}
);
Post as a guest
Required, but never shown
Sign up or log in
StackExchange.ready(function () {
StackExchange.helpers.onClickDraftSave('#login-link');
});
Sign up using Google
Sign up using Facebook
Sign up using Email and Password
Post as a guest
Required, but never shown
Sign up or log in
StackExchange.ready(function () {
StackExchange.helpers.onClickDraftSave('#login-link');
});
Sign up using Google
Sign up using Facebook
Sign up using Email and Password
Post as a guest
Required, but never shown
Sign up or log in
StackExchange.ready(function () {
StackExchange.helpers.onClickDraftSave('#login-link');
});
Sign up using Google
Sign up using Facebook
Sign up using Email and Password
Sign up using Google
Sign up using Facebook
Sign up using Email and Password
Post as a guest
Required, but never shown
Required, but never shown
Required, but never shown
Required, but never shown
Required, but never shown
Required, but never shown
Required, but never shown
Required, but never shown
Required, but never shown